fulloreo.blogg.se - Projectile intersection vector 2d

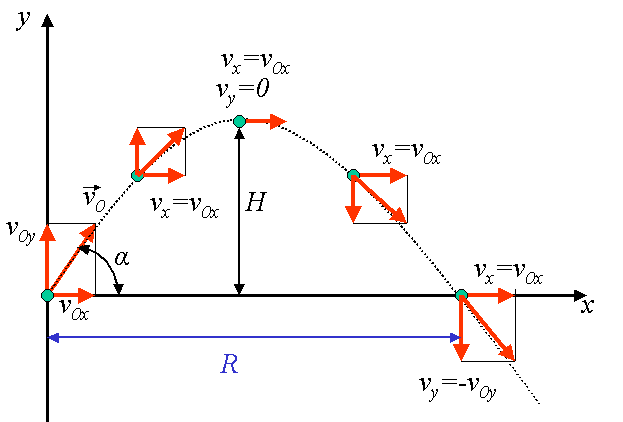
Since B and A have two components, we can translate this into V (xB-xA, yB-yA) However, this vector is pretty much useless because the length of it is the length of the line between A and B. $\cos^2\beta+\sin^2\beta=1$ to find a quartic equation in $\sin\beta$.Įxplicit solutions can be found with the aid of a software, but they are too long to be of any help: in practice I think it's better to solve the equation numerically. Suppose you throw some object near the surface of the earth. To get the vector between A and B, you have to do the following formula: V B - A. Students should be familiar with the concepts of velocity and acceleration, at the vector level, and have a working knowledge of the kinematical equations. One can extract $\cos\beta$ from there and insert the result into

$\vec v_0$ = the initial velocity of the projectile (the player's velocity).

But finding that path has turned out to be really difficult, which makes me think I must be overlooking something obvious. If the intersection point was beneath the Y-position of the pillar (the green line), it means we. Once fired, it finds a path to the target. Thats where the bullet hits the representation of the pillar. I'm working on a 2D game where one of the weapons available to the player is the classic "heat seeker" projectile.